963.minimum area rectangle ii(最小面积矩形 ii)

Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.

If there isn’t any rectangle, return 0.

给定在 xy 平面上的一组点，确定由这些点组成的任何矩形的最小面积，其中矩形的边不一定平行于 x 轴和 y 轴。

如果没有任何矩形，就返回 0。

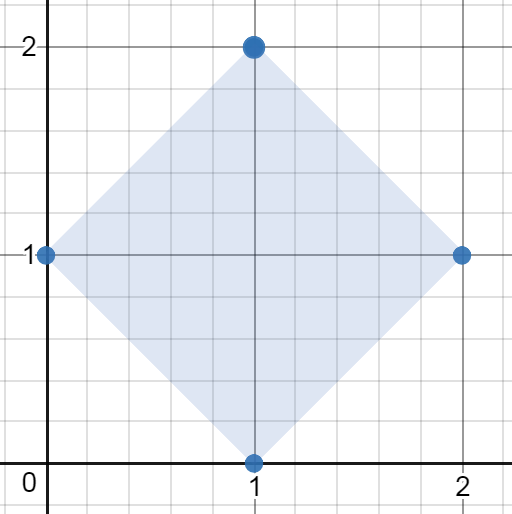
Input: [[1,2],[2,1],[1,0],[0,1]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.

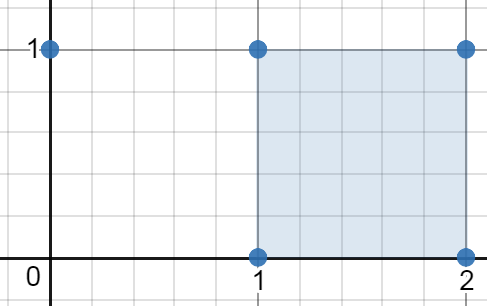
Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]
Output: 1.00000
Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.

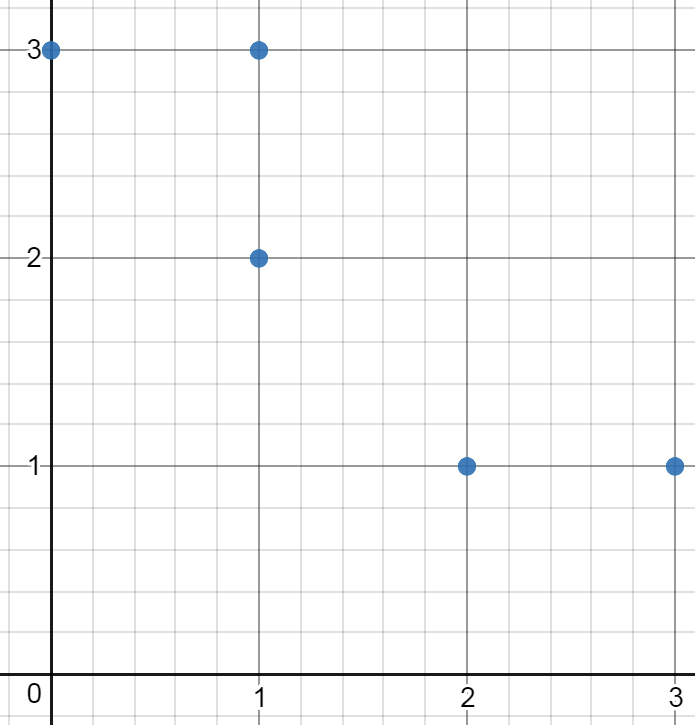
Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]
Output: 0
Explanation: There is no possible rectangle to form from these points.

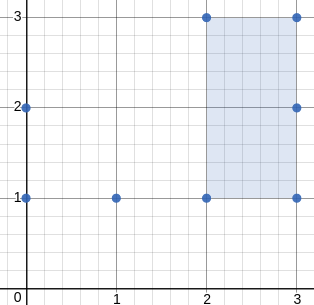
Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.

• 1 <= points.length <= 50
• 0 <= points[i][0] <= 40000
• 0 <= points[i][1] <= 40000
• All points are distinct.
• Answers within 10^-5 of the actual value will be accepted as correct.

• updating（Solution）

class Solution(object):
def minAreaFreeRect(self, points):
    EPS = 1e-7
    points = set(map(tuple, points))

    ans = float('inf')
    for p1, p2, p3 in itertools.permutations(points, 3):
        p4 = p2[0] + p3[0] - p1[0], p2[1] + p3[1] - p1[1]
        if p4 in points:
            v21 = complex(p2[0] - p1[0], p2[1] - p1[1])
            v31 = complex(p3[0] - p1[0], p3[1] - p1[1])
            if abs(v21.real * v31.real + v21.imag * v31.imag) < EPS:
                area = abs(v21) * abs(v31)
                if area < ans:
                    ans = area

    return ans if ans < float('inf') else 0