
Defination Two events $A$ and $B$, with $P(B)>0$, the conditional probability of $A$ given $B$ , denoted by $P(A|B)$, is defined as :
- $P(A)$: prior probability
- $P(A|B)$: posterior probability
Bayes’ Rule & LOTP
Chain Rule
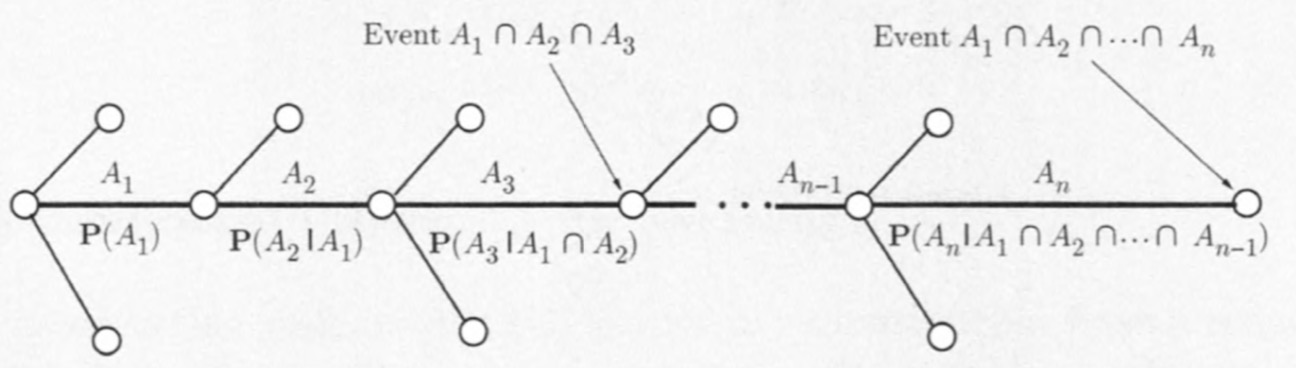
Bayes’ Rule
LOTP (Law of Total Probability)

Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, with $P(A_1)>0$, Then :
Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, for any event $B$ such that $P(B) > 0$, we have :
Conditional Probabilitiy
Conditional Probability is also the probability, so it inherent the property of probability (suppose the sample space is $S$):
- $P(S|E) = 1$ and $P(emptyset|E) = 0$
- if events $A_1,…$ are disjoint, then $P(cup_{j=1}^{infty}A_j|E) = sum_{j=1}^{infty}P(A_j|E)$
- $P(A^c|E) = 1 - P(A|E)$
- Inclusion-Exclusion : $P(Acup B|E) = P(A|E) + P(B|E) - P(Acap B|E)$
Bayes’ Rule with Extra Condition:
Theorem: Provided that $P(Acap E)>0$ and $P(Bcap E)>0$, we have:
LOTP with Extra Condition:
Theorem: Let $A_1,A_2,…,A_n$ be the partition of the sample space $S$, with $P(A_i cap E) >0$, Then:
Approaches for $P(A|B,C)$
Independence of Events
Independence of Two Events
Defination: Events $A$ and $B$ are independent if
Independence vs Disjointness
- $A,B$ is disjoint : $P(Acap B) = 0$
- $A,B$ is independent : $P(A) = 0, P(B) = 0$
Conditional Independence
Defination: Events $A$ and $B$ are conditionally independent given E if:




近期评论