
有这样一个问题
有$n$个台阶,你每次只能走一阶或两阶,有多少种走法。
假设$n=5$
手玩一下会发现5 = 1 + 1 + 1 + 1 + 15 = 1 + 1 + 1 + 25 = 1 + 2 + 1 + 15 = 2 + 1 + 1 + 15 = 1 + 1 + 2 + 15 = 2 + 1 + 25 = 2 + 2 + 15 = 1 + 2 + 2
综上一共八种方法。
其中第一步走$1$阶的有$5$种方案,第一步走$2$阶的有$3$种方案,可以把走法进行分类:
·第一步走$1$阶,则还有$n-1$阶要走,有$f(n-1)$种方案
·第一步走$2$阶,则还有$n-2$阶要走,有$f(n-2)$种方案
得到了$f(n)$的递推式:$f(n) = f(n-1) + f(n-2)$
边界为$f(0)=1,f(1)=1$
还有这样的
有一对兔子,每只兔子从第二个月开始每月产雌雄各一的一对新兔子,第$n$个月后有几对兔子。
再次手玩发现

每只兔子出生的那一个月还不能繁殖后代,所以第$n$月的兔子总数为$f(n)=f(n-1)+f(n-2)$即上个月能生产后代的兔子数即这个月新出生的兔子数再加上上个月已经存在的兔子
满足F_1 = F_2 = 1,F_n = F_{n - 1} + F_{n-2}的数列叫做斐波那契数列(Fibonacci)
Code
递归操作
1 |
int Fib(int n){ |
因为使用了递归,所以会出现重复计算。
更高效的方法是递推:
1 |
int Fib[2333333]; |
当然还有更高效的算法,但是我太弱了还不会。
Fibonacci数列的数学性质
与黄金分割比的关系
观察数列的前几项:1 1 2 3 5 8 13 21 34 55 89...
求相邻两项的商得到1 0.5 0.67 0.6 0.625 0.61538 0.61904 0.617647 0.618181818 0.61797752808
取极限后相邻两项的商为黄金分割比,这个性质也可以根据通项公式得到
科普通项公式$f(n)=frac{1}{sqrt5}[(frac{1+sqrt5}{2})^n-(frac{1-sqrt5}{2})^n]$
整除性
每$3$个连续的斐波那契数有且只有一个被$2$整除,
每$4$个连续的斐波那契数有且只有一个被$3$整除,
每$5$个连续的斐波那契数有且只有一个被$5$整除,
每$6$个连续的斐波那契数有且只有一个被$8$整除,
每$7$个连续的斐波那契数有且只有一个被$13$整除,
……
每$n$个连续的斐波那契数有且只有一个被$f(n)$整除。
杨辉三角

如图,每条斜线上的数之和构成了Fibonacci数列。
可以理解为把杨辉三角依次下降,将同一行的数字加起来
1 |
1 |
下降->
1 |
1 ------1 |
即有$f(n)=C_{n-1}^0+C_{n-2}^1+…+C_{n-m-1}^m$
欧几里得算法的时间复杂度问题
求两个数的最大公约数,用辗转相除法
1 |
int (int a, int b){ |
最坏情况下,若$a$较小,需计算$n$次,则$a>f(n-1)$
虽然不怎么懂,但还是很神奇的样子
氢原子能级问题
留给物理竞赛了
植物生长
科学家发现,一些植物的花瓣、萼片、果实的数目以及排列的方式上,都有一个神奇的规律,它们都非常符合著名的斐波那契数列。例如:蓟,它们的头部几乎呈球状。在下图中,你可以看到两条不同方向的螺旋。我们可以数一下,顺时针旋转的(和左边那条旋转方向相同)螺旋一共有13条,而逆时针旋转的则有21条。此外还有菊花、向日葵、松果、菠萝等都是按这种方式生长的。

还有菠萝、松子等,也都符合这个特点,一般会出现34,55,89和144这几个数字。

Fibonacci Tree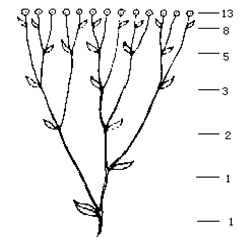
Fibonacci螺旋
斐波那契螺旋又称黄金螺旋,在自然界中广泛存在。如图是一个边长为斐波那契数列的正方形组成的矩形。
$f(1)^2+f(2)^2+…+f(n)^2=f(n)cdot f(n+1)$
贝壳螺旋轮廓线



是不是很神奇,这应该就是数学之美吧
世事洞明皆数学,留心处处是文章。
参考文献及图片来源
斐波那契数列为什么那么重要,所有关于数学的书几乎都会提到?
斐波那契数列在杨辉三角中的应用
“杨辉三角”中的一些秘密
手残党手动制作




近期评论