
i.i.d sequence of random variables: too restrictive assumption
completely dependent among random variables: hard to analysis
balance between complete independence & complete dependence
Classification of Markov Process
- Discrete-Time Markov Chain: Discrete $S$ & Discrete $T$
- Continuous-Time Markov Chain: Discrete $S$ & Continuous $T$
- Discrete Markov Chain: Continuous $S$ & Discrete $T$
- Continuous Markov Chain: Continuous $S$ & Continuous $T$
Definition (Markov Chain)
A sequence of random variables $X_0,X_1,X_2,…$ taking values in the state space ${1,2,…,M}$ is called Markov Chain, the event $X_i+1$ only influenced by $X_i$
$$P(X_{n+1}=j|X_n = i,X_{n-1}=i_{n-1},…,X_0=i_0) = P(X_{n+1}=j|X_n=i)$$
Definition (Transition Matrix)
Let $X_0,X_1,X_2,…$ be a Markov Chain with state space ${1,2,…,M}$, and let
$q_{ij} = P(X_{n+1}=j|X_N=i)$ be the transition probability from state $i$ to state $j$. The $M times M$ matrix $Q=(q_{ij})$ is called transition matrix of the chain.
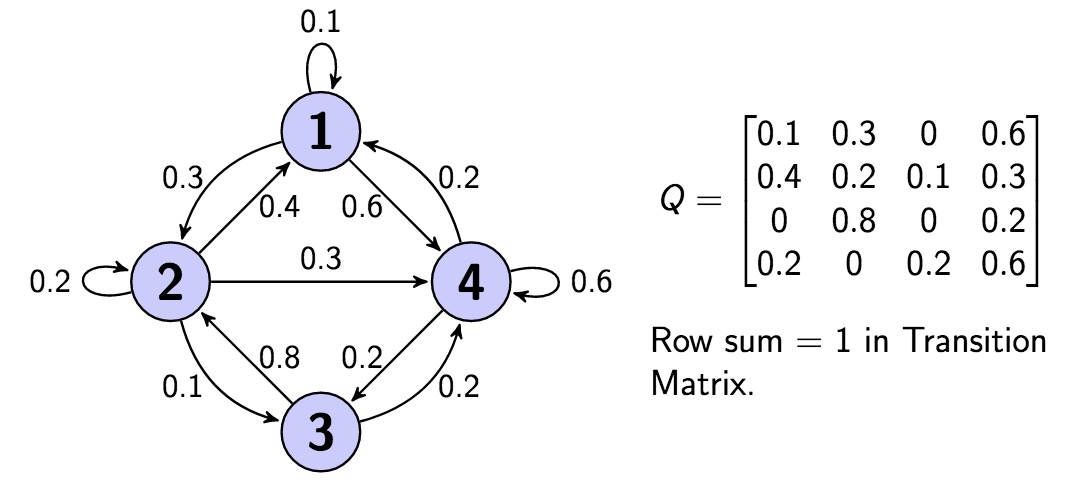
Definition (n-step Transition Probability)
The n-step transition probability from $i$ to $j$ is the probability of being at $j$ exactly $n$ steps after being at $i$. Denote this by $q^{(n)}_{ij}$
$$q^{(n)}_{ij} = P(X_n=j|X_0=i)=sum_{kin S} q^{(1)}_{kj} q^{(n-1)}_{ik}$$
which implies
$$Q^n = Q^{n-1}cdot Q$$
Theorem (Chapman-Kolmogorov Equation)
$$q_{ij}^{(n+m)} = sum_{kin S} q^{(n)}_{ik} q^{(m)}_{kj}$$
Example (Toss A Coin till HH Appear)
This problem can be formulated as a 3-state markov chain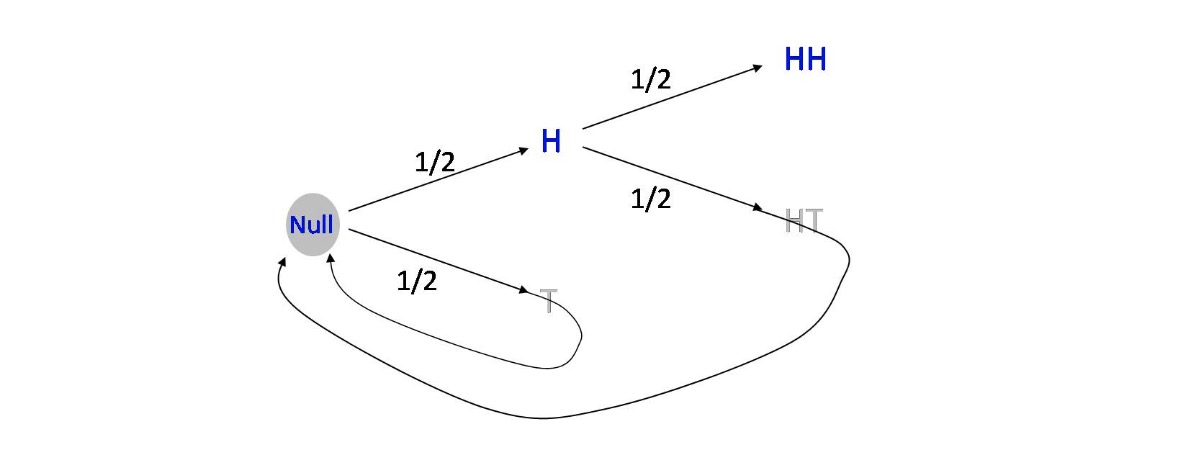
The Transition graph is equivalent to
Let $e_s = E[text{waiting time for HH|initial state = s}]$, then we have
$$begin{align}
e_{Null} &= frac{1}{2} (1+e_{Null})+frac{1}{2} (1+e_H) \
e_H &= frac{1}{2} (1+e_{HH}) + frac{1}{2} (1+e_{Null})\
e_{HH} &= 0
end{align}$$
Example (Toss A Coin till HTHT Appear)
Let see a more complicate case , this can be done by establish a linear equation

Classification of States
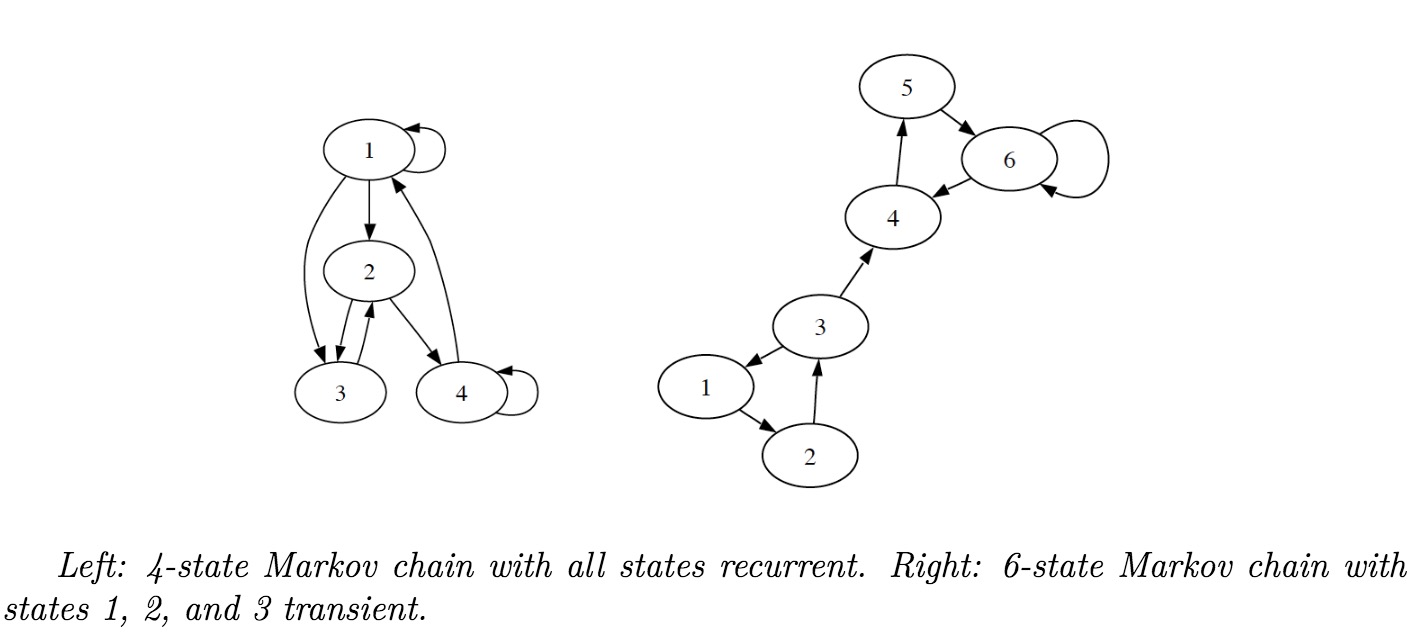
Definition (Recurrent and Transition States)
- Recurrent State $i$ of Markov chain have the probability of $1$ eventually return to $i$
- Transient Other-wise, the state is Transient
Definition (Irreducible & Reducible Chain)
- Irreducible any state $i$ and $j$, possible to go from $i$ to $j$ in a finite number of steps.
- Reducible not irreducible
Theorem (Irreducible Implies All States Recurrent)
In an irreducible Markov Chain with a finite state space, all states are recurrent
Example (Coupon Collector)
We want to collect all $C$ types coupons, Let $X_n$ be the number of distinct coupon types in our collection after $n$ attempts. Then $X_0,X_1,…$ is a Markov Chain on the state space ${ 0,1,…,C }$
Definition (Period)
The period of state $i$ in a markov chain is the gcd of the possible numbers of steps can return to $i$ when starting at $i$. A state is called aperiodic if its period equals 1, and periodic otherwise.
.




近期评论