
Convex Hull(凸包)
若S为平面上的点集{p1,p2,…,pn},convex hull of S, denoted by conv(S),是包含S的全部点的最小polygon。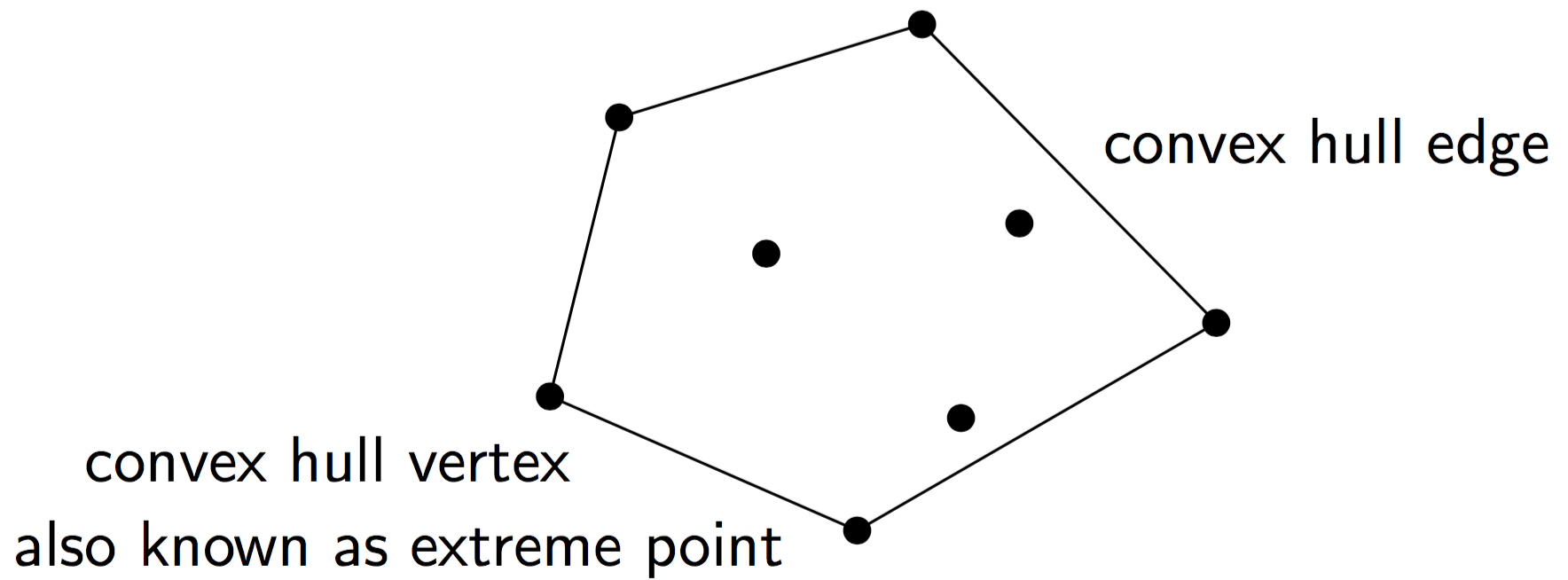
Graham’s Scan
为简化为题,将平面旋转某个角度,使得任意两个点的x坐标都不同。
找出leftmost与rightmost的点,这两点将conv(S)分为upper hull和lower hull两部分。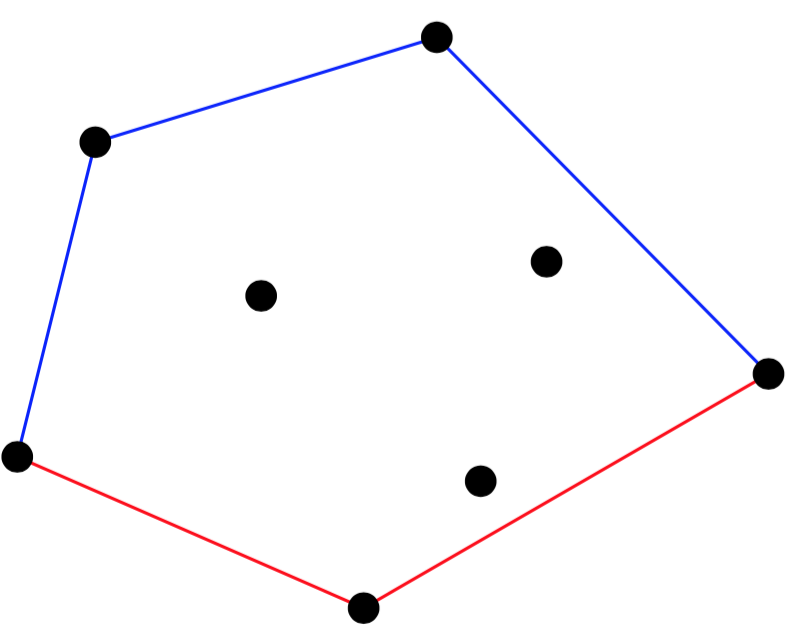
一次Graham’s scan可以找出upper hull,然后同理可得lower hull。
(1)将S按x坐标排序。
(2)从左到右scan S。初始化一个stack D。
(3)设r为下一个scan的点:
(i)若D中为空,或只有一个点,则将r放入D。
(ii)若D中有两个或以上的点,则设top的点是q,第二top的点是p,
若p→q→r是右转,则将r放入D;
若p→q→r是左转或直线,则将q pop出来,重复(i)到(ii)知道r被放入D中。
(4)遍历完S后D即为upper hull。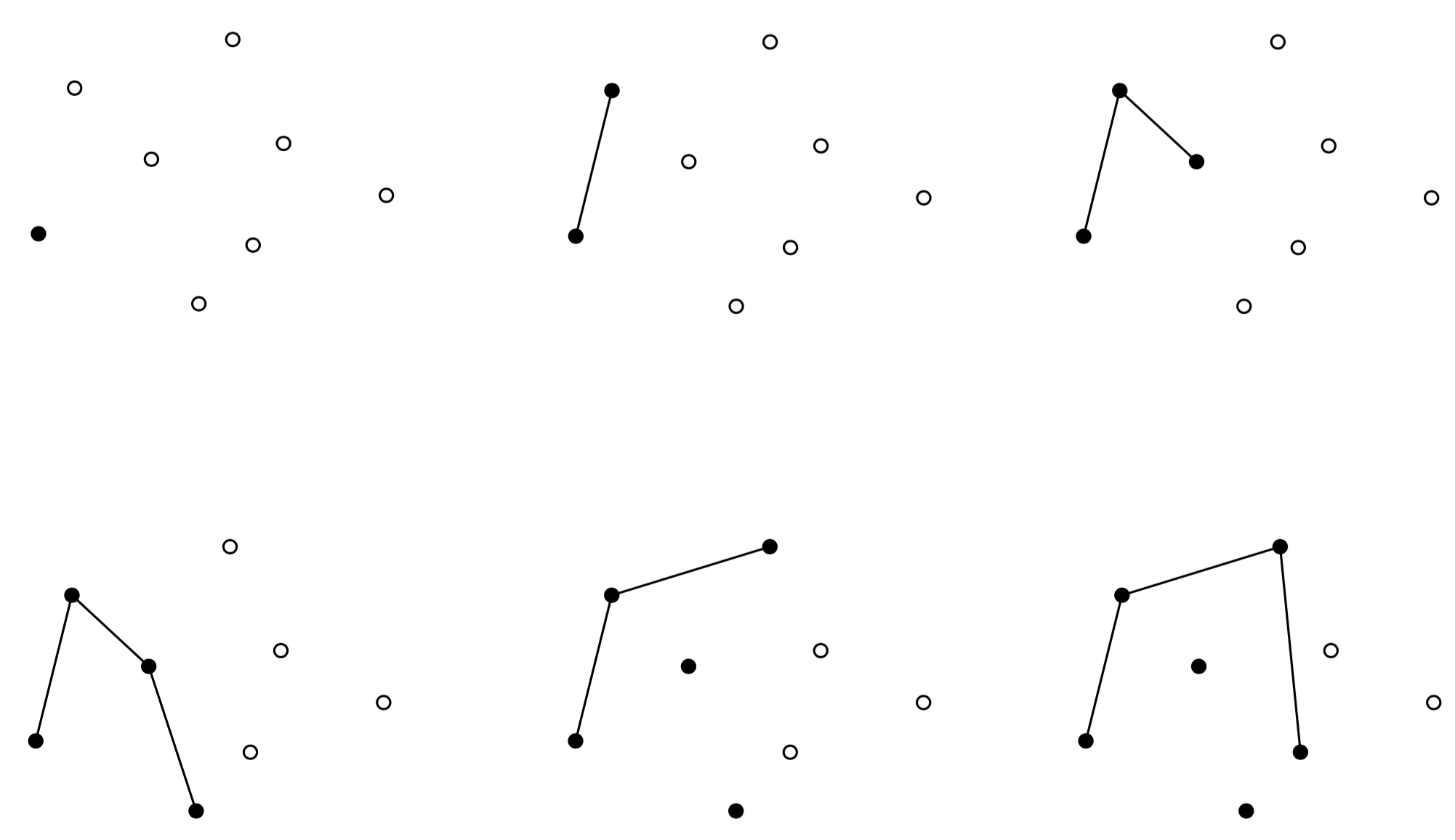
右转的判断:
先求pq的直线方程y = k(x - px) + py, k = (qy - py) / (qx - px)。
然后把rx代入,判断k(rx - px) + py > ry是否成立。
或者用行列式: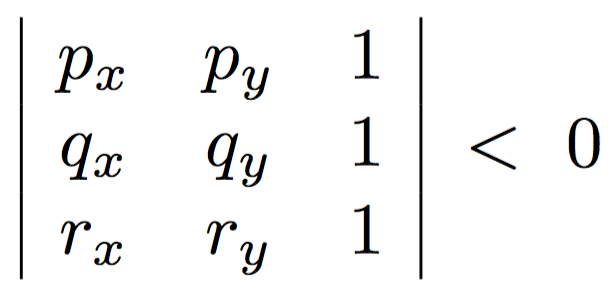
Time complexity取决于排序时间,n log(n)。
分治法
把S排序后分为左右两份,对每份计算其conv,之后合并。
设左半部分为S1,右半部分为S2,S1的rightmost的点是p,S2的leftmost的点是q。规定p在下面遍历中逆时针移动,q则顺时针移动。
(1)若r为q的下一个移动点,判断p→q→r是否右转,若否则q移动到r。不断重复直到p→q→r是右转。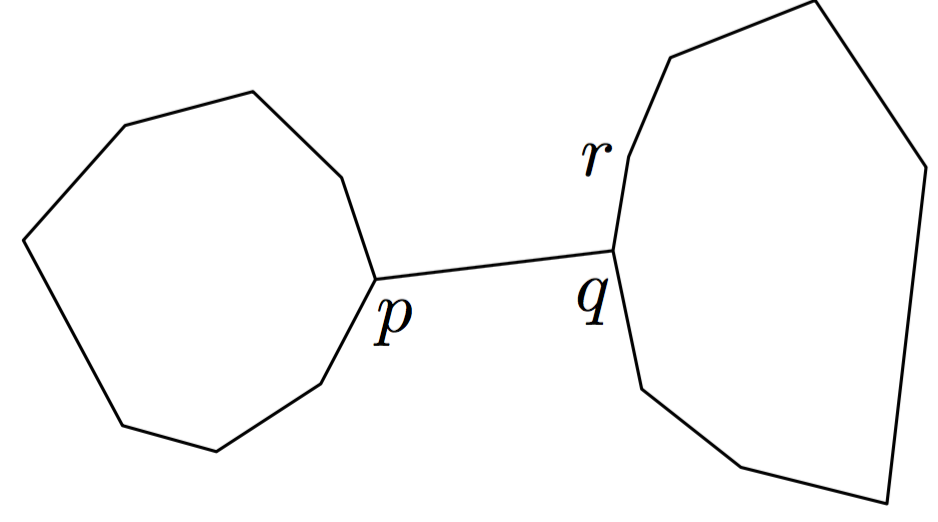
(2)移动p,另r为p的下一个移动点,若q→p→r是右转,若否则p移动到r。不断重复直到q→p→r不是右转。
(3)若不能再移动p或q了,则pq is the upper outer tangent of conv(S1) and conv(S2)。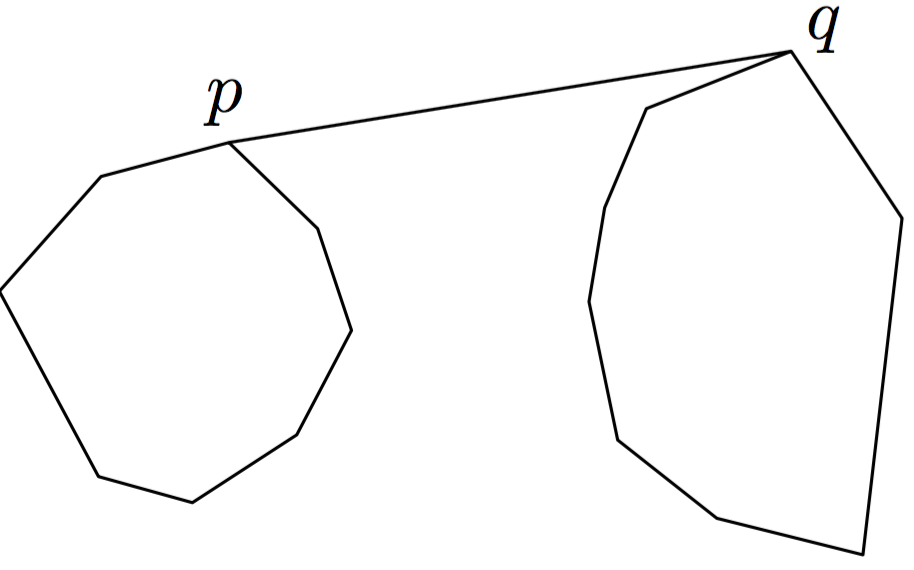
同理可得lower outer tangent of conv(S1) and conv(S2)。
Time Complexity: 合并需要O(n),则整个算法需要n log(n)。




近期评论